
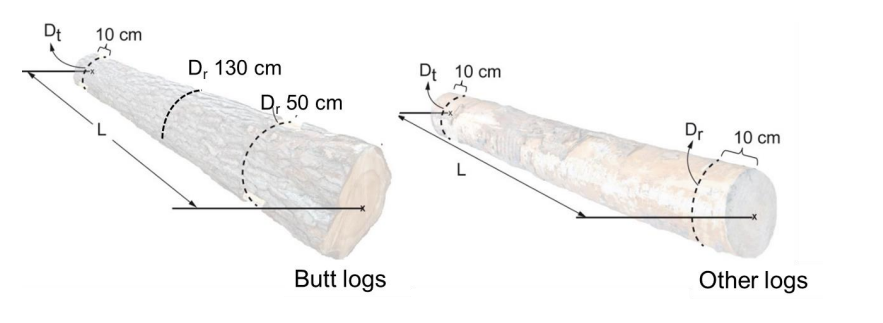
The formula for calculating the top-butt-measured volume is given by:
\[ V = \frac{\pi}{4} \cdot L \cdot (\alpha D_r^2 + (1 - \alpha) D_t^2) \cdot 10^{-8} \]
where:
The value of \( \alpha \) is determined based on the top diameter and length of the log:
Let's assume the following values:
Using the formula:
\[ V = \frac{\pi}{4} \cdot 500 \cdot (0.485 \cdot 30^2 + (1 - 0.485) \cdot 20^2) \cdot 10^{-8} \]
Calculating step-by-step:
\[ 30^2 = 900 \]
\[ 20^2 = 400 \]
\[ V = \frac{\pi}{4} \cdot 500 \cdot (0.485 \cdot 900 + 0.515 \cdot 400) \cdot 10^{-8} \approx 0.00252 m³sub \]
The calculated top-butt-measured volume is approximately 0.00252 m³sub.