
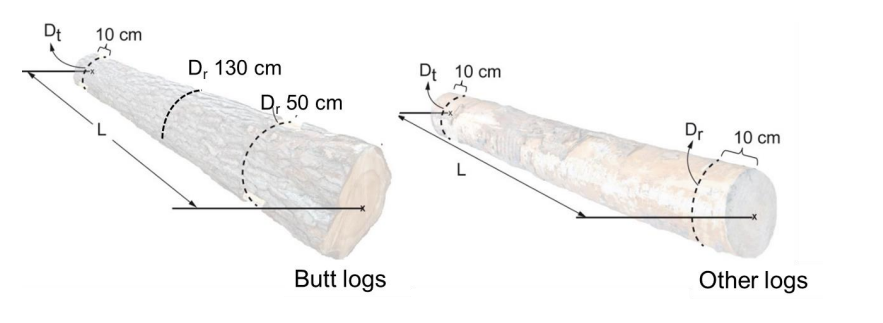
In top-butt measurement, the log volume is determined using two diameter measurements, one from the butt end and one from the top end. This type of top-butt measurement is used for pine and spruce assortments suitable for sawing, and is expressed in m3 sub2 . The measurement is based on the diameter 130 cm from the butt on butt log types, and 10 cm from the butt on other log types, and the diameter 10 cm from the top and log length in the volume calculations. The measurement method has different functions for tree species (pine and spruce) and log type, and is adapted for assortments suitable for sawing
The log type is divided into butt log and other log types, and is determined objectively through the tapering at the butt end. All logs where the difference in diameters over bark 10 cm from the butt compared with 50 cm from the butt exceeds 13 mm are defined as butt log types, and all logs with up to 13 mm difference are defined as other log types
The formula for calculating the top-butt-measured volume is given by:
For Butt Log Type:
\[ V_b = \alpha_1 + \frac{\alpha_2 \cdot D_t^2 + \alpha_3 \cdot D_{r130}^2}{4} \cdot \pi \cdot L \cdot 10^{-8} + \alpha_4 \cdot D_{r130} \]
For Other Log Type:
\[ V_b = \frac{\alpha_2 \cdot D_t^2 + \alpha_3 \cdot D_{r10}^2}{4} \cdot \pi \cdot L \cdot 10^{-8} \]
where:
The values of \( \alpha_1, \alpha_2, \alpha_3, \alpha_4 \) are determined based on the tree species and log type:
| Tree Species | Log Type | \( \alpha_1 \) | \( \alpha_2 \) | \( \alpha_3 \) | \( \alpha_4 \) |
|---|---|---|---|---|---|
| Pine | Butt Log | -0.0136 | 0.314 | 0.637 | 0.0001149 |
| Pine | Other Log | - | 0.524 | 0.473 | - |
| Spruce | Butt Log | -0.0180 | 0.340 | 0.604 | 0.0001589 |
| Spruce | Other Log | - | 0.606 | 0.410 | - |
Let's assume the following values:
Using the formula for Butt Log Type:
\[ V_b = -0.0136 + \frac{0.314 \cdot 20^2 + 0.637 \cdot 100^2}{4} \cdot \pi \cdot 500 \cdot 10^{-8} + 0.0001149 \cdot 100 \]
Calculating step-by-step:
\[ 20^2 = 400 \]
\[ 100^2 = 10000 \]
\[ V_b = -0.0136 + \frac{0.314 \cdot 400 + 0.637 \cdot 10000}{4} \cdot \pi \cdot 500 \cdot 10^{-8} + 0.0001149 \cdot 100 \]
\[ V_b \approx -0.0136 + \frac{125.6 + 6370}{4} \cdot \pi \cdot 500 \cdot 10^{-8} + 0.01149 \]
\[ V_b \approx -0.0136 + 1623.9 \cdot \pi \cdot 500 \cdot 10^{-8} + 0.01149 \]
\[ V_b \approx -0.0136 + 0.0255 + 0.01149 \approx 0.0234 \, \text{m}^3_{\text{sub}} \]
The calculated top-butt-measured volume is approximately 0.0.234 m³sub.